Úvod

1.10. Stejnosměrný proud

Elektrický proud je tedy vlastně přenos nabitých částic z jednoho místa na jiné (povětšinou z jednoho pólu zdroje do druhého). V době, kdy ještě nebylo známo, které částice se na tom podílejí, říkali někteří, že "prochází od + k - " a jiní zase že "naopak". Protože v tom byl samozřejmě zmatek, byl nakonec stanoven dohodnutý směr proudu a ten zní: El. proud prochází od kladného pólu zdroje směrem k zápornému. Dnes již víme, že je tomu právě naopak, ale dohoda nebyla změněna, protože by to díky následujícímu zmatkováni způsobilo více škody než užitku a přitom by se vlastně nic nezměnilo, nehledě na to, že pro výpočty je kladné znaménko také poměrně příjemné. Při dalších úvahách o proudu se tedy budeme tvářit, jako že proud opravdu prochází zmíněným směrem.
Proud I (jednotka Ampér A) jako veličina udává jaké množství elektronů daným místem projde (tedy vlastně jak velký náboj je transportován) za jednotku času, podobně jako průtok vody je projdivší množství vody za jednotku času.
Napětí U (jednotka Volt V) mezi dvěma místy udává, jak silně se budou elektrony snažit dostat z jednoho do druhého, podobně jako je tomu s tlakem zmiňované vody. Můžeme tedy říci, že: Napětí je síla, která uvádí do pokybu proud. Pro další úvahy dále nutno podotknout, že kromě U a I se pro napětí a proud používá u a i s tím, že UI udává velikost napětí a proudu pokud se jedná o statické, tedy časově neměnné hodnoty, zatímco ui se používá pro vyjádření okamžitých hodnot v závislosti na čase.
Relativnost napětí        Napětí je pojem relativní, protože záleží na tom, vůči čemu jej vztahujeme, neboť se jedná o rozdíl potenciálů. Na obrázku vidíme názorný příklad: Pokud za vztažný poteniál budeme považovat spoj mezi třívoltovými bateriemi, budou napětí na jednotlivých svorkách taková, jaká jsou tam napsána. Ale můžeme klidně třeba prohlásit, že 0 je ta úplně spodní svorka a budou správná napětí v prvním sloupci tabulky.
       Pro dobré pochopení vztahu mezi napětím a proudem je také vhodná poučka: Napětí je a proud prochází. Proto má smysl věta říkající, že v zásuvce je 230 V, ale nemá smysl věta říkající, že v zásuvce je 10 A, protože proud tam není, neboť může pouze procházet. Věta pro jistotu nemá smysl ještě z dalšího důvodu, protože nebude procházet takový proud, jaký je napsán na jističi, ale takový, jaký odebírá spotřebič.
Vodivost G (jednotka Siemens S) je vlastnost vodiče, která nám říká, jak velký proud bude procházet při jednotkovém napětí. Mělo by býti celkem jasné, že silnější a kratší vodič bude mít vyšší vodivost, než tenčí či delší.

I = U.G [A, V, S]

Odpor R (jednotka Ohm W) je pravým opakem vodivosti, tedy její převrácenou hodnotou a je tedy schopnost vodiče bránit se průchodu proudu. - Říkáme, že je průchodu proudu kladen odpor.

R = 1/G [W, S]

Vztah mezi napětím proudem a odporem je jedním z nejdůležitějších vztahů v elektrotechnice a jmenuje se Ohmův zákon: Proud je přímo úměrný napětí a nepřímo úměrný odporu. Jedná se tedy v podstatě o slovní vyjádření vzorce:

I = U/R [A, V, W]

Který si lze lidověji vyložit jako: "Čím větší napětí, tím větší proud a čím větší odpor, tím menší proud." Obdobně jako všechny ostatní fyzikální zákony, i Ohmův zákon pro své tři veličiny platí třísměrně a tedy lze též tvrdit, že "Čím větší proud, tím větší napětí a čím větší odpor, tím větší napětí", nebo že "Čím větší napětí, tím větší odpor a čím větší proud, tím menší odpor.", což lze vyjádřit vzorci:

U = IR [V, A, W]       R = U/I [W, V, A]

Tip: Již od základní školy je všem vtloukáno do hlavy, že před výpočtem je nutno všechny hodnoty převést na základní jednotky. - To ovšem není tak docela pravda: Stačí totiž, aby se řády předpon navzájem vykrátily. Správný výsledek tedy dostaneme i když budeme počítat bez převádění rovnou v volty, kiloohmy a miliampéry, což je v elektronice zjevně nejčastější kombinace (Pokud používáme vysoké odpory, můžeme používat i megaohmů a mikroampérů.).
Dalšími ze základích elektrotechnických zákonů jsou Kirchhohfovy zákony:
1. Součet proudů v uzlu je roven nule. - Nebo jinak: Součet proudů do uzlu vtékajících je roven součtu proudů z uzlu vycházejících. (Tomuto zákonu budeme pro přehlednost v dalším textu říkat proudový.)
2. Součet napětí v obvodu je roven nule. - Nebo jinak: Součet napětí zdrojů ve je roven součtu úbytků na spotřebičích. (Tomuto zákonu budeme pro přehlednost v dalším textu říkat napěťový.)
Napětí a proudy v obvodu        Na obrázku vidíme názornou ukázku, jak Ohmův zákon a zákony Kirchhohfovy fungují. (Zeleně jsou číslovány uzly, napětí jsou červená a proudy modré.) Za nulu jsme si zvolili záporný pól spodní baterie (uzel 4), takže na uzlu 1 jsou 3 V a na uzlech 2, 3 a 7 je 6 V. Napětí na odporu 1 W jsou tedy 3 V a dle Ohmova zákona jím prochází proud 3 A Tento proud je samozřejmě stejně velký před i za ním, tedy od uzlu 2 do uzlu 5. Obdobná je i situace odporu 2 W, kterým ale prochází jen 1,5 A.
       Nyní se budeme věnovat stření části obvodu, tedy odporům 4 a 6 Ohmů, které jsou zapojeny mezi uzly 3 a 4: Vzhledem k tomu, že uzel 3 je přímo spojen s kladným pólem horní bareie, je na něm 6 V. Na uzlu 4 je 0 V, tedy rozdíl mezi nimi činí 6 V. Protože se obvod v bodě 6 nevětví (tedy tento není uzlem), prochází oběma odpory (4 a 6 Ohmů) stejný proud, který je právě tak velký, aby součet úbytků na nich byl roven 6 V, tedy je dán součtem odporů a šesti volty. Součet je zjevně 10 W, takže skrz ně prochází 6/10 = 0,6 A. Nyní můžeme vypočíst napětí v bodě 6: Dejme tomu, že vypočteme úbytek na odporu 6 W, tedy 0,6 krát 6 = 3,6 V. Stejně můžeme i vypočíst úbytek na 4 W, tedy 0,6 krát 4 = 2,4 V a odečíst od 6 V, čímž též dostáváme 3,6 V.
Nejjednodušší je situace v části s bodem 7, kterým nemůže procházet proud, neboť vodič z něj vycházející nevede nikam. Proto je také nulový úbytek napětí na sedmiohmovém odporu a na konci vodiče je tedy 6 V
Nyní zkusíme zjistit, jaký proud prochází vodičem mezi uzly 1 a 5, což nejsnáze půjde po vypočtení proudů procházejících bateriemi, nebo odpory 1 a 2 ohmy. Vzhledem k tomu, že jednoohmovým rezistorem prochází 3 A a dvouohmovým jen 1,5, musí vodičem odcházet zbývajících druhých 1,5 A.
Nebo můžeme spočítat proudy procházející bateriemi: Protože z uzlu 2 vychází 3 A dolů a 0,6 A doprava, musí do něj z baterie vcházet 3,6 A. Do uzlu 4 vstupuje 0,6 A zprava a 1,5 A shora, do dolní baterie tedy musí jít 2,1 A. Jestliže do uzlu 1 zespoda vstupuje jen 2,1 A a shora odchází 3,6 A, musí do něj zároveň vstupovat i zbývajících 1,5 A.
Pokud čtenáři tato úvaha není jasná, doporučuje se, aby si ji přečetl vícekrát, neboť úvahy o napětích a proudech jsou při návrhu el. obvodů nejdůležitější. Jestiže ji ale přeci jen nechápe, pak pro něj prozatím bude platit "třetí Kirchhohfův zákon", který říká, že cesty proudů jsou nevyzpytatelné...

Zdroje napětí a zdroje proudu
Zdroj napětí důvěrně známe z běžného života: Jeho cílem je, aby dodával stabilní výstupní napětí a to pokud možno nezávisle na velikosti odebíraného proudu. Mezi takové zdroje patří rozvodná síť, různé baterie a články, zdroj ve vašem PC... a pod. Existuje ale ještě druhý typ zdrojů zvaný zdroj proudu, který se chová právě opačně: Snaží se aby dodával stabilní proud a to nezávisle na úbytku napětí, jaký při něm vznikne na spotřebiči. Těchto zdrojů je ve skutečnosti daleko více, neboť v téměř každém analogovém integrovaném obvodu je jich větší počet. Krom toho se v poněkud robustnějším (a tedy viditelném) provedení používají jako jeden z druhů nabíječek.
Zdroje napětí a proudu
Pro snažší pochopení oba zdroje vidíme na obrázku, kde horní řada znázorňuje různými odpory zatížený desetivoltový zdroj napětí a dolní jednoampérový zdroj proudu za stejných podmínek. Vidíme, že na zdroji napětí je stále stejné napětí a podle odporu zátěže se mění velikost procházejícího proudu, zatímco zdrojem proudu prochází stále stejný proud a zdroj dává takové napětí, aby tento proud odporem "protlačilo".
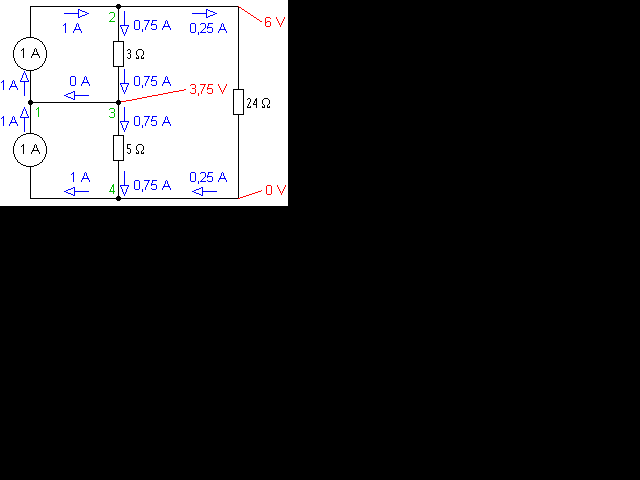Napětí a proudy v obvodu        Nyní zkusíme analyzovat obvod, který je vyobrazen vlevo a je záměrně velmi podobný předchozímu obvodu s bateriemi a odpory: Základní rozdíl je, že baterie (tedy zdroje napětí) byly nahrazeny zdroji proudu. Obvod začneme analyzovat od uzlu 1: K němu je sdola i shora připojen proudový zdroj dodávající 1 A. Protože oba proudy jsou shodné, vodorovným vodičem do uzlu 3 nemůže procházet žádný proud. Je tedy jasné, že na obvod můžeme nahlížet, jako kdyby tento vodič vůbec neobsahoval. Potom tedy můžeme tří a pětiohmový odpor sdružit v jeden osmiohmový. Paralelně k němu je v uzlech 2 a 4 připojen odpor 24 W, což je třikrát více než 8, takže proud se musí rozdělit v poměru tři čtvrtiny a jedna čtvrtina. Dvacetičtyřohmovým odporem tedy bude procházet 0,25 A a dvěma zbylými 0,75 A.
       Možností odstranění vodiče mezi uzly 1 a 3 se dostáváme k řešení chování obvodu na dalším obrázku: Pokud budou odpory vlevo a vpravo tvořit děliče se stejným dělícím poměrem, bude napětí na obou koncích prostředního odporu shodné a jím tedy nebude procházet proud, pročež jej můžeme z dalších úvah vynechat.
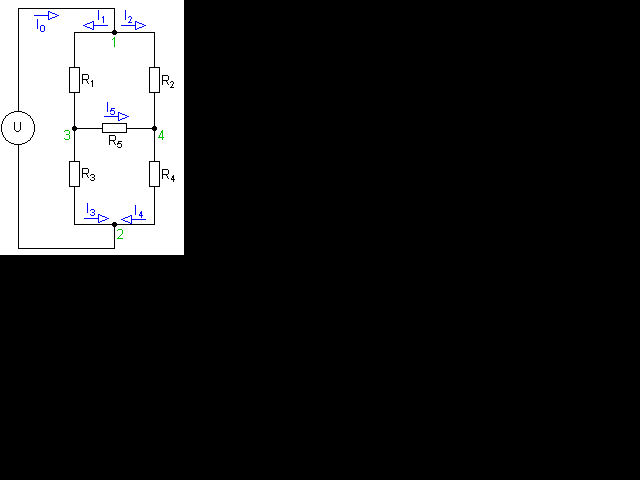K zanedbatelnosti některých hodnot        Tato varianta ovšem není v běžném životě příliž pravděpodobná, ale naštěstí není jediná, protože se velmi často spokojíme s výsledkem, který má omezenou přesnost a tak můžeme prostřední odpor vynechat i pokud jsou dělící poměry krajních děličů blízké a tedy rozdíl napětí uzlů 3 a 4 tak malý, že proud je zanedbatelný. Obdobné situace mohou nastat i při řádové odlišnosti některého z odporů od ostatních: Pokud je bude totiž výrazně převyšovat, proud jím procházející bude zanedbatelný a odpor můžeme zase vynechat. Pokud bude naopak výrazně nižší, způsobí proud jím procházející značné přiblížení napětí na jeho koncích, takže když jej naopak nahradíme vodičem, nic znatelného se nestane.
       Právě správné rozhodování jaké hodnoty můžeme zanedbat a jaké nikoli má zásadní vliv na funkčnost, reprodukovatelnost a stabilitu námi navrženého obvodu. Zdálo by se, že dnes, tedy v době rychlých a stále rychlejších počítačů můžeme všechno vypočítat s velkou přesností a zanedbatelnosti hodnot vůbec nemusíme věnovat pozornost. Toto zdání je ovšem zcela klamné, neboť i nejmodernější simulační programy pracují se zjednodušenými voltampérovými charakteristikami u nelineárních prvků (např. diody a tranzistory), protože ve složitějších obvodech by byla výpočetní náročnost neúnosně vysoká. - Důsledkem je, že zejména obvody, ve kterých výsledná funkce závisí na větším počtu vzájemě se ovlivňujících úbytků na přechodu báze-emitor v tranzistorech budou ve skutečnosti pracovat úplně jinak, než uvidíme v simulátoru. Proto ani při použití simulátorů není vhodné zapomínat na správné určení zanedbatelnosti hodnot a vlivů.
Jordanova křivka a zobecněný proudový Kirch. zákon
Jordanova křivka

       Pokud přeci jen budeme chtít přesně spočítat proudy a napětí v obvodu, který je podobný tomu na předchozím obrázku, lze k tomu použít metod odvozených přímo z Kirchhohfových zákonů; nejprve ovšem zavedeme malé rozšíření: Proudový Kirchhofův zákon neplatí jen pro uzly, ale i pro libovolné části jakéhokoli obvodu ohraničené souvislou hranicí (které říkáme Jordanova křivka), resp. pro proudy tuto hranici protínající, přičemž vůbec nezáleží na tom, co se uvnitř skrývá.

Obvodové rovnice

       
(pokračování příště)

<< Zpět      Obsah      Další >>