Účinnost nabíjení kondenzátoru
Problém nabíjení kondenzátoru se často, dlouze a většinou nepříliš úspěšně řeší v různých internetových
i hospodských diskusích. V následujících odstavcích se pokusím tento problém vyřešit dostatečně
jednoduše a srozumitelně.
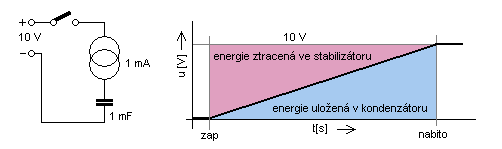
Na obrázku vidíme situaci, kdy ideální kondenzátor o kapacitě 1 mF (milifarad) nabíjíme z ideálního zroje
napětí, přes ideální proudový stabiliátor nastavený na 1 mA. Již ze samotné definice kapacity je celkem jasné,
že za daných okolností napětí na kondenzátoru lineárně poroste, až konečně po uplynutí 10 s bude nabito
a proud přestane procházet. Je také jasné, že energie v něm uložená bude
E = 1/2 C U2 [J, F, V - nebo mJ, mF, V]
tedy
E = 0,5 . 1 mF . (10 V)2 = 50 mJ
Z pohledu zdroje odebíráme při napětí 10 V proud 1 mA po dobu 10 s:
E = P t [J, W, s] = U I t [J, V, A, s - nebo mJ, V, mA, s]
tedy
E = 10 V . 1 mA . 10 s = 100 mJ
Energetická účinnost nám tedy vychází přesně 50 %. Protože nabíjíme stabilním proudem, je příkon ze zdroje
stále stejný a můžeme snadno sledovat jeho rozložení mezi kondenzátor a stabilizátor (výkon je zde rozdělen ve stejném poměru, jako napětí): V počátečním okamžiku
je na kondenzátoru nulové napětí a celý odebíraný výkon se tedy ztrácí na stabilizátoru. Jak se kondenzátor nabíjí,
roste napětí a tím také výkon jím absorbovaný, zatímco ztráty na stabilizátoru se stejnou rychlostí
snižují. V každém okamžiku je tedy ukládán výkon úměrný napětí na kondenzátoru a ztrácí se výkon úměrný rozdílu
od napětí napájecího. Jak je na obrázku naznačeno, výsledná plocha pod křivkou odpovídá uložené energii a plocha
nad křivkou odpovídá ztrátám.
Pokud si nyní graf rozpůlíme v okamžiku, kdy napětí dosáhne poloviny (5 V), takže již byla uložena čtvrtina
požadované energie (12,5 mJ) a uplynula polovina času, zjistíme, že za první polovinu se spotřebovalo
50 mJ a uložilo 12,5, zatímco za druhou polovinu času se spotřebuje také 50 mJ, ale uloží se z toho
37,5. Je tedy zřejmé, že v první polovině je průměrná účinnost 25 % a ve druhé 75 %.
Nyní budeme uvažovat, jak to dopadne, pokud bychom použili jiný průběh nabíjení: Zkusme dejme tomu nabíjet nejprve proudem 0,5 mA a v druhé polovině 2 mA. Myslím, že je zřejmé, že k dosažení poloviny napětí
dojde až po dvojnásobném čase (10 s) a zbývající část naopak zabere poloviční dobu (2,5 s). Ovšem
z energetického hlediska se nic nezmění, v první části zase spotřebujeme 50 mJ a nabijeme 12,5 a v druhé části
spotřebujeme 50 a nabijeme 37,5. Pokud bychom rychlé a pomalé nabíjení prohodili, dostaneme zjevně stejný výsledek
a je jastné, že stejný výsledek dostaneme při jakémkoli průběhu nabíjecího proudu, tedy například i když
proudový stabilizátor nahradíme odporem (v takovém případě bude ovšem vlivem postupného klesání proudu úplné nabití
trvat nekonečně dlouho).
A nešlo by to nějak obejít a účinnost zvýšit?
První možností je, pořídit si větší kondenzátor, s tím, že jej nikdy nebudeme zcela vybíjet. Použijeme-li
v našem pokusu kondenzátor o kapacitě 2 mF, bude napětí na něm po odebrání 50 J ještě 7,07 V, takže dobíjení
na 10 V začne s účinností skoro 71 %. Celková účinnost tedy dosáhne 85 %. Pokud bychom kapacitu
dále zvyšovali, účinnost dále poroste a to libovolně blízko ke 100 %. Tohoto principu využívá skupina měničů napětí, označovaná spínané kondenzátory
(swithed capacitors). V nich běžné kapacity jsou z pohledu naší úvahy dokonce nejméně řádově „předimenzované“.
Typickým příkladem této skupiny je např. konvertor napětí ve známém IO MAX232.
Pro mnohé překvapivým výýsledkem této úvahy může být zjištění, že účinnost těchto měničů nijak zvlášť
nezávisí na odporu spínacího prvku, dokud tento není tak vysoký, aby zamezil dostatečnému dobití za jeden
cyklus a tím vedl k citelnému poklesu výstupního napětí.

Dále můžeme použít indukčnost. - Zbývající část energie se neztratí, ale zůstane uchována v podobě magnetického pole.
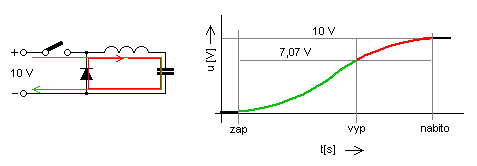
Při pokusu zobrazeném na následujícím obrázku nejprve zapnutím spínače začne procházet zvolna rostoucí proud naznačený zelenou šipkou.
Nyní počkáme, až obvod ze zdroje odebere požadované množství energie (polovina bude v cícve a polovina v kondenzátoru) a spínač zase vypneme. Od tohoto okamžiku bude postupně klesající proud (červená šipka) přenášet energii z cívky
do kondenzátoru, dokud nebude cívka zcela vybitá. Teoretická účinnost tohoto řešení je přesně 100 %.
Ukládání energie v podobě proudu procházejícího indukčností je běžnou součástí principu činnosti většiny měničů,
jejichž schéma obsahuje cívku, nebo transformátor.
Kdybychom vypnuli spínač později, můžeme dokonce docílit vyššího napětí. Například vypnutí až po nabití kondenzátoru
na 10 V by mělo za následek, že energie bude dvojnásobná, takže napětí po vyprázdnění cívky dosáhne 14,1 V.
Pokud bychom s vypnutím ještě dále otáleli, napětí na kondenzátoru poroste také a dostoupá ještě výše, protože po celou
dobu bude stále čerpána energie ze zdroje. Zcela limitní je pak pro naše zapojení vypnutí až po samovolném zániku proudu
(vypínač pak můžeme nahradit diodou), který nastane až při dosažení 20 V, tedy až bude kondenzátor obsahovat
čtyřnásobek energie při 10 V.
Pro energii v cívce platí vzorec:
E = 1/2 L I2 [J, H, A]
(edizon zavináč seznam tečka cz, icq 771 04328)





